Por: Guillermo Anaya Quintal
Jefe del Programas Académicos de Posgrado
Universidad Virtual del Estado de Guanajuato

Resumen
La modelación de sistemas basados en constructos humanos es sumamente compleja pues su comportamiento obedece a una gran diversidad de factores, así como la interacción entre ellos. Además, dichos factores cambian con el transcurso del tiempo debido a la transformación cultural y social de la cual surgen. En la presente investigación se desarrolla un modelo de comportamiento del componente tendencial del Índice de Precios y Cotizaciones (IPC) de la Bolsa Mexicana de Valores (BMV) empleando una aproximación polinómica, así como algunos principios de econofísica. El resultado obtenido es sumamente preciso con un error inferior al 0.2%.
Abstract
The modeling of systems based on human constructs is extremely complex because their behavior is due to a great diversity of factors as well as the interaction between them. In addition, these factors change over time due to the cultural and social transformation from which they arise. In the present investigation, a behavioral model of the trend component of the Price and Quotation Index (CPI) of the Mexican Stock Exchange (BMV) is developed using a polynomial approximation as well as some principles of economics. The result obtained is extremely accurate with an error of less than 0.2%.Introducción
Las Ciencias de la Administración, como parte de las Ciencias Sociales, tienen por campo de estudio sistemas que son constructos humanos en su mayoría. Si excluimos las comparaciones etológicas de las formas de organización nos encontramos que todos los sistemas estudiados son producto de la invención humana. El Índice Dow Jones Industrial Average (DJIA), la tasa de matrimonios, la moda o el Producto Interno Bruto (PIB), por poner algunos ejemplos, son conceptos que mueven a la toma de decisiones, pero todos son constructos humanos producto de determinadas convenciones y necesidades sociales con reglas de interacción y una lógica propia, así como de significados asociados a su comportamiento.
Estos constructos pueden ser o no una invención deliberada de una parte de grupo social determinado, pero su aceptación, proliferación de uso y significado final por la mayoría del grupo siempre será un acuerdo social, el cual por cierto tampoco requiere, necesariamente, ser explícito y/o intencional. Como los sistemas sociales (y por consecuencia los sistemas administrativos) están conformados por estos constructos humanos, la interacción entre ellos suele ser compleja lo cual dificulta su estudio y modelaje. Los resultados de estos sistemas sociales no dependen únicamente del comportamiento aislado de los constructos que los conforman, sino que las interacciones, e incluso la retroalimentación entre los elementos que constituyen dichos constructos, pueden provocar resultados inicialmente inesperados e incluso paradójicos de acuerdo su concepción establecida. Su esencia parece de naturaleza caótica.
Además, los constructos humanos son cambiantes debido a la dinámica social de los grupos humanos aumentando con ello la dificultad de su análisis. Un concepto y su significado pueden variar asombrosamente rápido a través del tiempo mientras que otro puede permanecer sin grandes cambios en lapsos muy largos comparativamente hablando. Incluso algunas teorías psicológicas y antropológicas hablan de arquetipos sociales inmutables a través del tiempo y de naturaleza genérica a toda la humanidad.
Debido a las características antes mencionadas es difícil poder llegar a un modelo basado en fórmulas determinísticas fijas que puedan proporcionar una descripción de comportamiento de estos constructos sociales a diferencia de las Ciencias Naturales.
Como se mencionó anteriormente, el modelaje de tendencias sociales abarca muchas áreas de interés para las Ciencias de la Administración como su aplicación a nivel implantación de innovaciones en una empresa u organización dada, la mercadotecnia de un producto o servicio, las condiciones socioeconómicas y políticas de una región o país, así como aspectos de económicos y financieros internacionales lo cual constituye todo un campo de estudio por sí mismo.
El objetivo de la presente investigación es elaborar un modelo de comportamiento del componente tendencial del IPC utilizando una técnica de agrupación en el periodo comprendido de 2002 al 2015.
La pregunta de investigación es ¿cómo se puede modelar el comportamiento del componente tendencial del Índice de Precios y Cotizaciones (IPC) de la Bolsa de Valores mexicana? La respuesta tentativa es a través de un modelo polinómico de segundo grado alternante.
Desarrollo (Teoría o Marco Teórico)
Bunge (1985) en su libro Economía y Filosofía define a los modelos como sistemas hipotético – deductivos que describen porciones o aspectos del mundo natural y social. Los modelos difieren de las teorías en tres aspectos: primero, su dominio es más reducido que en las teorías; segundo, los modelos son representaciones simplificadas o idealizadas del objeto que representan; y tercero, a diferencia de las teorías no necesariamente contienen leyes. Ahora, para construir un modelo según el autor se puede iniciar de cero (él le denomina libre) o se puede construir tomando como base alguna teoría (le denomina ligado).
Desde mediados de los cincuenta se han elaborado criterios y modelos para la toma de decisiones. Dentro de los modelos probabilísticos existen las decisiones bajo incertidumbre las cuales se presenta que el resultado (estado de la naturaleza) puede variar, pero la persona que toma la decisión no quiere o puede determinar las probabilidades de los estados de la naturaleza resultantes. Para ello se han desarrollaron varios criterios como por ejemplo el de Laplace, el cual se resume en <<si nada sé, entonces todo es igualmente posible>>. En este modelo para la toma de decisiones bajo incertidumbre se introduce un concepto fundamental el cual es la función de utilidad considerada como una medida de satisfacción o el aspecto atractivo del dinero. Al colocar esta función de utilidad en el eje y y la posible ganancia en el eje x se obtienen las funciones de utilidad adversas al riesgo (curva cóncava hacia abajo), propensas al riesgo (curva cóncava hacia arriba) o indiferentes (línea recta) (Eppen, Gould, Schmidt & Moore, 2000).
Ahora respecto al modelaje de tendencias sociales. Según Ogburn (2000), las tendencias sociales tienen un gran valor científico por ser neutrales sus resultados, ya la interpretación subjetiva que se haga de ellos será con base en la perspectiva adoptada, pero la tendencia es objetiva. Además, su análisis es versátil pues típicamente se estudian con base en datos cuantitativos, sin embargo, es posible hacerlo en términos descriptivos no cuantitativos. De hecho, el autor atribuye a la descripción verbal más que a la estadística el hecho que se haya adoptado el término. Aunque advierte del riesgo de considerar una tendencia a la descripción verbal de observaciones casuísticas sesgadas por el observador cuando no cuenta con datos sistemáticos. El autor nos advierte respecto a dos aspectos vitales de las tendencias, el hecho que haya movimientos por debajo o por encima de una línea de tendencia se le denomina fluctuación y es común que se confunda con una tendencia. Ahora, respecto a la pregunta de cuánto tiempo se requiere para determinar una tendencia, el autor aconseja que al menos se tomen en cuenta cinco o más ciclos de fluctuaciones, entiendo por ciclo de fluctuaciones un movimiento por encima y por debajo de la tendencia para volver a remontar.
Para propósitos prácticos una tendencia es un movimiento a largo plazo en una serie de tiempo que a veces se comporta como una línea recta o una curva suave. Existen otras opciones que también toman en cuenta la curvatura, pero que presentan una tasa de decrecimiento gradual en la parte final, como las funciones en forma de ‘S’ tales como la curva de tendencia de Gompertz y la curva de tendencia logística. En todas ellas, el problema es determinar el horizonte de pronóstico pues eventualmente dejarán de tener validez. Las tendencias según los autores resultan útiles para analizar incrementos en productividad derivados de la adopción de una nueva tecnología que conllevan cambios en los estilos de vida, incrementos de la población que ocasionan incrementos de la demanda de productos y servicios, el poder de compra de una moneda que afecta las variables de compra por casusas inflacionarias, incremento en la aceptación del mercado de un producto o servicio innovador, entre otros fenómenos que se pueden expresar como series de tiempo (Hanke y Wichern, 2010).
Una herramienta sumamente útil para la comprensión y modelado de comportamientos de sistemas sociales es la Econofísica, disciplina que aplicar los principios de la física a los fenómenos económicos (Gosh, 2013). De acuerdo con Ausloss (2000), la Econofísica es una ciencia incipiente y, aunque difícilmente logrará el estatus de ciencia exacta, existe un gran potencial para explicar algunos fenómenos complejos de la Economía y de las Ciencias Sociales en general. Existen numerosos ejemplos de la aplicación de conceptos de la física, como el momentum newtoniano aplicado a la conducta (Nevin, Mandell y Atak, 1983).
Metodología
Se analiza solamente el componente tendencial del IPC basado en datos mensuales. Para ello se obtiene el componente tendencial por un método tradicional de suavizamiento exponencial aditivo de doce periodos (uno por cada mes) utilizando el complemento para el MS Excel denominado XLSTAT obteniéndose los datos de la tendencia desde enero del 2002 a diciembre 2015. Los datos del componente tendencial se le restan el dato actual al anterior (velocidad) y a los resultados a su vez se vuelve a restar el resultado actual al anterior (aceleración); se agrupan los signos resultantes como indicio de fluctuación.
El método elegido es exclusivamente cuantitativo, no experimental pues se estudian cantidades y no se tiene control sobre la variable en cuestión. El tipo es longitudinal o evolutivo de tendencia debido a que precisamente se estudian las fluctuaciones que presenta el componente tendencial de dicho índice a través del periodo establecido. Se asume que en el periodo establecido el componente tendencial del IPC presenta un comportamiento modelable no lineal. Por otro lado, para lograr el objetivo de la investigación, la muestra de datos se obtuvo del indicador SF4782 de Banxico (www.banxico.org.mx) con los niveles mensuales del IPC (índice general) de julio del 2001 a junio del 2016. Los resultados esperados son un modelo de comportamiento probablemente fraccionado (no puede reducirse a una única ecuación fácilmente manejable para todo el periodo, pero sí como una sucesión de ecuaciones simples).
Resultados
Siguiendo el método establecido, se agrupó el comportamiento con base a la aceleración de las fluctuaciones del componente tendencial del IPC con un comportamiento polinómico de segundo grado con abertura alternante hacia arriba y hacia debajo de la parábola asociada a la ecuación como se muestra en la tabla 1 a continuación.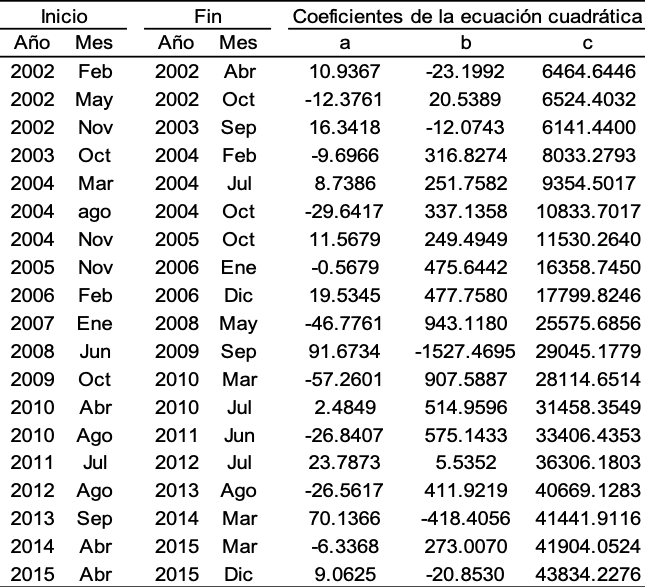
Tabla 1. Coeficientes por fluctuación del 2002 al 2015
Nota: Nótese la alternancia del signo del componente cuadrático a través del periodo de estudio completo (incluyendo la validación). Continuando con la metáfora física, nótese que en los periodos correctivos con caída y en su subsiguiente recuperación el coeficiente cuadrático es mayor (abertura amplia de la parábola) y asociado con una aceleración grande, así como el coeficiente lineal asociado con la velocidad inicial.
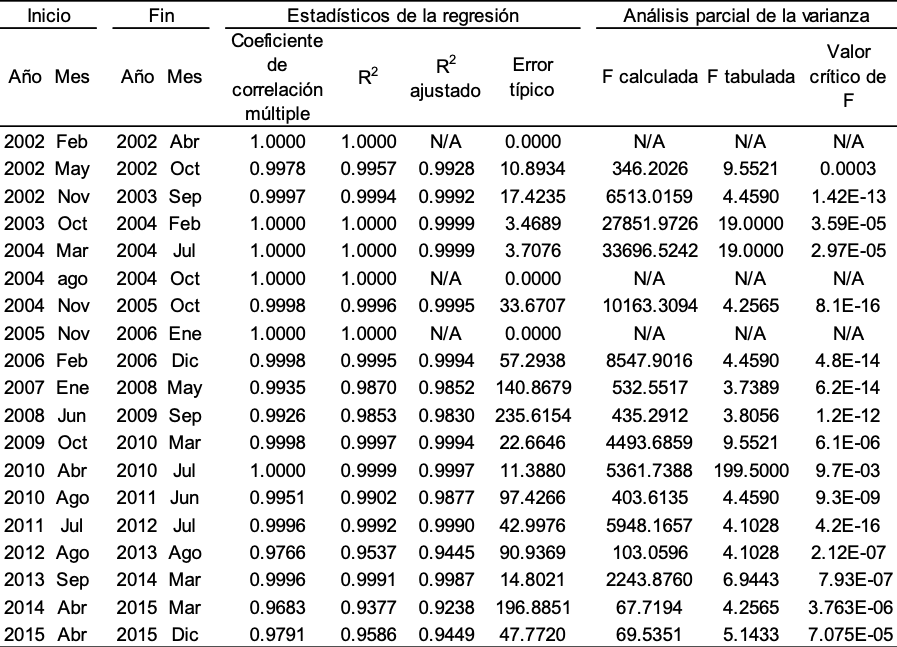
Tabla 2. Validación de la modelación del IPC por segmentos de parábola del 2002 al 2015.
Nota: Resalta que el ajuste de la R2 ajustada menor es de 0.9238, pero la mayoría están muy cercanos a uno, indicio del gran ajuste del modelo al comportamiento real.
Utilizando los valores de F calculada y tabulada, así como el valor crítico de F se prueba la hipótesis siguiente:
Ho: β1 = β2 = 0
Ha: al menos una βj ≠ 0
En todos los casos de la tabla 2 la F tabulada es menor que la F calculada, así como el valor crítico de F siempre es menor a 0.05 por lo anterior se rechaza Ho y se acepta Ha. Además, el valor p asociado y los valores de la F tabulada, así como el valor crítico de F tomando una significancia del 5% indican que los valores que el comportamiento del componente tendencial del IPC agrupado en relación con el tiempo aportan información significativamente mejor que solamente usar la media.
Por lo anterior se acepta el modelo del componente tendencial del IPC basado en ecuaciones polinómicas de segundo grado con alternancia en la abertura de la parábola hacia arriba y hacia abajo en la totalidad del periodo de estudio del 2002 al 2015. Para cerrar el objetivo, se evalúa la precisión del modelo aplicando medidas de error como la media porcentual absoluta media del 0.2216%, una desviación absoluta media de 59.3191 y una desviación cuadrática media de 9467.2754
Conclusiones
La modelación del comportamiento del componente tendencial del IPC respecto del tiempo a través de una sucesión de parábolas alternantes con abertura hacia arriba y hacia abajo basado en sus aceleraciones resulta ser una aproximación bastante aceptable dentro de los márgenes de confiabilidad y error establecidos. El ajuste de la curva mostrado gráficamente en la Tabla 1, aunado a las pruebas de hipótesis y magnitudes del error calculado constituyen un indicio que el modelo se desempeña bastante bien respecto al comportamiento real.
La línea de tendencia es sumamente útil para indicarnos hacia dónde se dirige el comportamiento de la variable que se estudia, pero el poder ajustar el comportamiento de todo el componente tendencial es aún más útil pues la gran mayoría de las teorías sobre el comportamiento de los mercados financieros hasta la fecha buscan explicar los fenómenos de forma global presentando aciertos parciales, cuando una aproximación más lógica es descomponer cada uno de los factores de la serie de tiempo– cíclico (en caso de existir), estacional, tendencial y aleatorio – y buscar variables explicativas para cada uno de ellos; al integrar los resultados es más probable lograr una explicación completa del comportamiento. Un fenómeno tan complejo como el comportamiento del IPC amerita este tipo de abordaje pues al descomponer en sus partes, ya se cuenta con el componente de tendencia, al hacerlo se obtiene también el componente estacional y solamente restaría determinar si existe componente cíclico y evaluar los factores asociados con el componente aleatorio. Actualmente ya se cuenta con dos de ellos.
Como se comentó desde un inicio, el estudio de las tendencias es de suma importancia para las Ciencias Sociales en general y para las Ciencias de la Administración en lo particular. Con los presentes resultados no se pretende sean extensivos en automático a todos los fenómenos sociales pues probablemente cada uno tenga fluctuaciones que respondan a otros modelos matemáticos dependiendo de su naturaleza, pero como primera recomendación de la línea de investigación establecida es aplicar la misma metodología a índices de bolsas de valores de otros países para evaluar si su comportamiento responde al mismo modelo que el establecido para el IPC.
Un hallazgo derivado de esta modelación apunta a su utilidad para evaluar el grado de estabilidad de una bolsa de valores y, probablemente del país pues este comportamiento puede ser un indicio de fluctuaciones bien definidas expansivas y correctivas cuando se considera que las condiciones son estables y comportamientos más erráticos cuando las condiciones apuntan a inestabilidad.
Por otro lado, este modelo presenta la ventaja de una aproximación diferente a los métodos econométricos tradicionales y sus dificultades asociadas como la multicolinealidad y la cointegración ya que si asumimos que una fluctuación se comportará de igual forma hasta que en su última etapa algo cambie (haciendo una metáfora de la primera ley de Newton) entonces si se encuentra aquello que cambia en esta última etapa se tendrá un método de pronóstico.
Referencias
- Ausloss, M. (2006). Econophysics of Stock and Foreign Currency Exchange Markets. En Econophysics and Sociophysics, Trends and Perspectives. 249-278. Alemania: WILEY-VCH.
- Bertalanffy, L. (1989). Teoría general de los sistemas. México: FCE.
- Bunge, M. (1985). Economía y filosofía (2ª Ed.). Madrid: Tecn
- Eppen, G., Gould, F., Schmidt, C., & Moore, J. (2000). Investigación de operaciones en la ciencia administrativa (5a Ed.). México: Prentice Hall.
- Gosh, A, (2013). Econophysics Research in India in the last two Decades. In IIM Kozhikode Society & Management Review, 2(2), 135-146. Recuperado de http://journals.sagepub.com/doi/abs/10.1177/2277975213507834?journalCode=ksma
- Hanke, J. & Wichern, D. (2010). Pronósticos en los negocios (9a Ed.). México: Pearson.
- Nevin, J., Mandell, Ch. & Atak, J. (1983) THE ANALYSIS OF BEHAVIORAL MOMENTUM. In Journal of the experimental analysis of behavior, 1. 49-59
- Ogburn, W. (2000) Tendencias sociales en Revista española de investigaciones sociológicas (REIS). Recuperado de http://www.reis.cis.es
Sobre el autor
Guillermo Anaya Quintal
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Doctor en Ciencias de la Administración titulado con mención honorífica por la UNIVA. Maestro en Administración, Maestro en Finanzas, Licenciado en Comunicación e Ingeniero en Comunicaciones y Electrónica. Actualmente se desempeña como Jefe de programas académicos de posgrado a cargo de la Maestría en Administración Estratégica en la UVEG. Ha desempeñado diversos cargos en instituciones públicas y privadas. Además, cuenta con una trayectoria de veinte años como consultor empresarial tanto para organizaciones gubernamentales en los tres niveles de gobierno como para la iniciativa privada. Es participante regular con investigación en los congresos realizados por ACACIA y el IMEF, así como coautor en dos libros editados por la UNAM.
![]() Descarga el artículo aquí
Descarga el artículo aquí






